大賀 成朗(物理学専攻 博士課程)
伊藤 創祐(生物普遍性研究機構/物理学専攻 准教授)
アルテミー コルチンスキー(生物普遍性研究機構 客員共同研究員)
発表のポイント
- 相互相関関数と呼ばれる統計量と熱力学的な駆動力の間に、普遍的な不等式関係が成り立つことを発見しました。
- この不等式は生体内の化学反応をはじめ広い範囲の系で成り立ち、振動や情報伝達など、相互相関関数と結びつく幅広い現象に対して普遍的な熱力学的限界を与えます。また、相互相関関数の実験データから駆動力の強さを推定する手法としても役立ちます。
- 生命をはじめとする非平衡系の設計原理を、個々の例を超えて統一的・普遍的に理解する助けになることが期待されます。
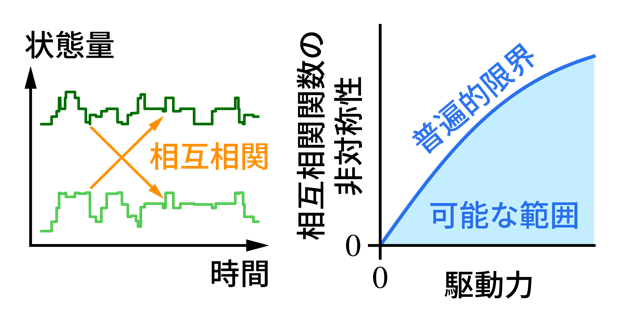
相互相関関数に対する普遍的限界
発表概要
東京大学大学院理学系研究科の大賀成朗大学院生、伊藤創祐准教授、アルテミー・コルチンスキー客員共同研究員は、相互相関関数の非対称性(注1)と呼ばれる統計量が、熱力学的な駆動力(注2)の大きさで決まる限界を決して超えないことを表す、普遍的な不等式を発見しました。
生命現象をはじめ、自然界に存在する多くの過程、例えば振動、循環、情報伝達、方向性のある運動などは、系にエネルギーを注入する熱力学的な駆動力の存在下で初めて可能になる非平衡現象です。こうした現象の大きさ(度合い)を定量的に表す指標の一つが、相互相関関数の非対称性です。本研究は、この非対称性を初めて普遍的かつ定量的な形で駆動力と結びつけ、一定の駆動力のもとで達成できる各現象の大きさの上限、すなわち現象の普遍的限界を発見しました。特に、本結果の帰結として、振動現象のコヒーレンス(規則正しさ)に対する普遍的限界が得られます。この帰結は、先行研究で予想されたものの6年間にわたり未証明であった普遍不等式を証明したことになります。これらの結果は、ゆらぎの熱力学(注3)と呼ばれる枠組みを用い、平面幾何の等周不等式(注4)を応用して導出されました。
本結果は幅広い系に対して普遍的に成り立ち、個別の系を超えた、非平衡現象の統一的な理解につながることが期待されます。さらに、実験で相互相関関数を測定することで、系に働く駆動力の大きさを推定する手法としても役立ちます。
本研究成果はPhysical Review Letters誌に掲載されました。また、特に注目すべき論文として顕彰されるEditors’ suggestionに選ばれ、アメリカ物理学会のオンラインマガジンPhysics Magazineにも取り上げられました。
発表内容
相関関数は、二つの量の間にどれだけ関係があるかを示す統計量です。物理学では、対象とする系の時間的・空間的構造を引き出すために、さまざまな量の間の相関関数が広く用いられてきました。このうち、任意の二つの状態量の間の相互相関関数は、平衡系(駆動力を受けない系)では、二つの状態量を入れ替えても値が変わらないという対称性を持つことが知られています。裏を返せば、相互相関関数の非対称性の存在は非平衡系(駆動力を受ける系)に固有の特徴であり、実験的に測定しやすい非平衡性の兆候として、生体内の化学反応系、生体の運動、乱流などで幅広く利用されてきました。しかし、相互相関関数の非対称性の具体的な大きさが、駆動力の大きさと定量的にどのように関係しているかは、いくつかの個別の系を除いて知られていませんでした。
相関関数と駆動力のように、出自の異なる二つの量どうしの普遍的な関係を調べるとき役立つ手法が、両者の間の不等式を導出することです。特に、ゆらぎの熱力学の分野ではさまざまな不等式が導出され、熱力学的な量と統計量の間の普遍的関係が発見されてきました。その代表例が、熱力学的不確定性関係(注5)です。これらの不等式は、一定の熱力学コストのもとで実現可能な現象の限界を示し、幅広い系が例外なく従う根源的な限界を与えます。では、相互相関関数の非対称性に対しても、熱力学的限界が存在するでしょうか?
本研究では、実際に相互相関関数の非対称性が従う新たな不等式を発見しました(図1)。この不等式は、各量の時間変化の速さを規定する自己相関関数(注6)で相互相関関数の非対称性の大きさを割って得られる普遍的な非対称性の指標が、サイクルの熱力学力(注7)と呼ばれる熱力学的駆動の強さで決まる限界を決して超えないことを示します。この結果は、離散状態間の遷移としてモデル化できる広い範囲の系の定常状態に適用でき、系の任意の状態量に対して成り立ちます。もともと、平衡系における相互相関関数の対称性は、平衡に近い系の普遍法則であるオンサーガーの相反関係(注8)の基礎となっています。これに対し本結果は平衡から任意に遠い領域でも成立するため、オンサーガーの相反関係の平衡から遠い領域への拡張としても解釈できます。

図1:本研究で得られた不等式の概念図
左:二つの状態量の間の相互相関関数。右:相互相関関数の非対称性に対する普遍的限界。
得られた不等式は一般的であるため、個別の系や状態量に適用することで、さまざまな物理的過程に対する限界を導くことができます(図2)。実際に本研究では、(i) 体内時計や細胞周期などのゆらぐ振動系のコヒーレンス(規則正しさ)に対する限界、(ii) 生体内の分子機構による情報伝達の大きさに対する限界、という二つの普遍的不等式を、一般的な不等式の帰結として導出しました。特に、(i)で得られる不等式は、先行研究で数値計算に基づいて予想されていたものの、数学的に完全な証明を与えることは6年間にわたって未解決問題でした。今回この予想に証明を与え、問題を解決したことになります。

図2:不等式の二つの帰結
(i) 体内時計などのゆらぐ振動系のイメージ。振動のコヒーレンス(規則正しさ)が、駆動力の大きさで制限される。(ii) 左:生体内の情報伝達のモデル。上段のOFF–ONの情報が、下段の0–1に伝達される。この情報伝達の度合いが、駆動力の大きさで制限される。右:ランダムなパラメータを用いた、情報伝達のモデルの数値シミュレーション。情報伝達の度合いを定量する相互相関関数の非対称性の指標(オレンジ)は、必ず普遍的限界(青)を下回る。
得られた不等式の応用はこれだけにとどまりません。さまざまな状態量の間の相互相関関数・自己相関関数を測定・計算し、その比から非対称性の指標を求めることで、系にはたらく駆動力の大きさの下限を見積もることができます。この応用は、駆動力の大きさを直接知るのが難しい複雑な系で、その構造を知るための重要なツールとなることが期待されます。必要な測定は短時間の相互相関関数と自己相関関数のみであり、多くの系で測定可能です。例えば、生体内の化学反応では、蛍光相互相関分光法と呼ばれる手法を用いて必要な相関関数が測定できます。
不等式の導出は、ゆらぎの熱力学の枠組みを平面幾何学と結びつけ、平面幾何学から新たなアイデアを取り入れることにより行われました。この導出では、相互相関関数と自己相関関数に、平面図形の面積と長さという新たな解釈を与えます(図3)。これにより、平面幾何学で知られる等周不等式と呼ばれる結果を応用することが可能になります。また、上で述べた応用(i)では、振動現象を特徴づける数学的な量である生成子の固有値を、相関関数を用いて書き表す式を新たに発見し、この式を利用しました。これらの新たな数学的手法は、熱力学の他の問題でも役に立つ可能性があります。

図3:不等式の導出に用いる平面幾何学
二つの状態量a, bの間の相関関数を、a–b平面上の長さ(青)と面積(オレンジ)として解釈する。この多角形の面積が、同じ周長を持つ正多角形より小さいことを述べるのが、等周不等式である。
本研究の結果は、非平衡系に対する統一的・普遍的な理解を深めるものです。駆動力の強さは、系にどれだけの強さでエネルギーを注入するかという、系の「設計書」の一項目といえるでしょう。このため、本研究の結果を幅広い現象に適用することで、生命現象をはじめとする非平衡系が諸現象を実現するために用いている設計原理を、普遍的に理解することにつながると期待されます。また、相互相関関数は幅広い物理学で用いられるため、本研究の数理的手法を応用して、さらに広い範囲の系に対して同様の普遍不等式を発見できるかもしれません。例えば、固体結晶の物性、量子デバイス、流体系など、他の物理系で同様の普遍法則を見出すことができれば、これらの系の普遍的な理解に役立つことも期待されます。さらに、こうした非平衡系の理解は、非平衡現象を制御して活用することにもつながると期待されます。
論文情報
-
雑誌名 Physical Review Letters 論文タイトル Thermodynamic bound on the asymmetry of cross-correlations
著者 Naruo Ohga*, Sosuke Ito, Artemy Kolchinsky
DOI番号
研究助成
本研究は、科研費「情報熱力学による生体情報処理の理論研究(課題番号:19H05796)」、「金融市場ミクロデータ解析によるHFTの実態調査と流動性シミュレーターの構築(課題番号:21H01560)」、「微分幾何学に基づいた非平衡熱力学における普遍的原理の探究(課題番号:22H01141)」、「ゆらぎの熱力学に基づく確率的コンピューティング基盤の創出(課題番号:23H00467)」、「非平衡熱力学の粗視化の諸手法:情報幾何学を用いた系統化と探索(課題番号:23KJ0732)」、科学技術振興機構ERATO特定領域調査(FS)「情報エネルギー変換(課題番号:JPMJER2204)」、UTEC-UTokyo FSI Research Grant Programの支援により実施されました。
用語解説
注1 相互相関関数の非対称性
相互相関関数とは、ある時刻で一つの量を測定し、一定時間後に別の量を測定したときの両者の相関である。二つの量が、時間変化を通じてどのように影響し合うかを反映する。相互相関関数の非対称性は、二つの量を測定する順番を入れ替えたときに、相互相関関数の値がどれだけ変わるかで定義される。↑
注2 熱力学的な駆動力
対象にエネルギーを注入し続ける機構を、熱力学的な駆動力という。例えば、生体内のエネルギー通貨であるアデノシン三リン酸の消費など化学反応による駆動、機械的に系を引っ張る外力による駆動、電位差を利用した電気的な駆動などがある。↑
注3 ゆらぎの熱力学
生命を構成する分子機械や微小な量子デバイスなど、ゆらぎを持つ小さな系の非平衡挙動を扱うために今世紀に発展した熱力学理論。近年日本語での教科書が相次いで出版されるなど、まさに現在確立されつつある分野である。従来の熱力学が平衡、あるいは平衡に近い状態を主に対象としたのに対し、ゆらぎの熱力学は平衡から任意に離れた領域を扱うことができる。↑
注4 等周不等式
平面の幾何学でよく知られているように、決められた外周の長さを持つ平面上のn角形のうちで、面積を最大にするのは正n角形である。この事実を不等式の形で述べ直したものが、等周不等式である。↑
注5 熱力学的不確定性関係
駆動力の存在下では、流れと散逸(エネルギー消費)が同時に生じる。流れの大きさと揺らぎの比が、散逸の大きさを超えないことを述べるのが、熱力学的不確定性関係である。2015年に提案されて以降、さまざまな変形や拡張が提案・導出されてきた。 ↑
注6 自己相関関数
一つの量を、ある時刻と一定時間後で2回測定したときの両者の相関。対象となる量の時間変化の速さや、その特徴を反映する。 ↑
注7 サイクルの熱力学力
対象とする系にはたらく熱力学的な駆動力の大きさの指標として、ゆらぎの熱力学で用いられる代表的な量。サイクルとは、系のある状態から出発して、同じ状態を通らずに最初の状態に戻ってくるまでの状態の列を指す。サイクルの熱力学力とは、系がこのサイクルを一周する間に系にはたらく全ての駆動力の総和である。これは、一周の間に消費されるエネルギー(正確には自由エネルギー)と等しい。系の詳細によらず、駆動力を与える外部系の性質で決まるため、解釈が容易で実験的にも扱いやすい量である。 ↑
注8 オンサーガーの相反関係
平衡に近い(弱い駆動を受けた)系に対して成り立つ、1930年代から知られる普遍法則。駆動力と流れの間の関係についてのある対称性を述べる。固体物性などのさまざまな系で、物理量を計算する際の基礎となっている。 ↑
からの記事と詳細 ( 非平衡状態の相関関数に潜む普遍法則 - s.u-tokyo.ac.jp )
https://ift.tt/XwCT7OG
No comments:
Post a Comment